Calculating the RMS of a Random Profile
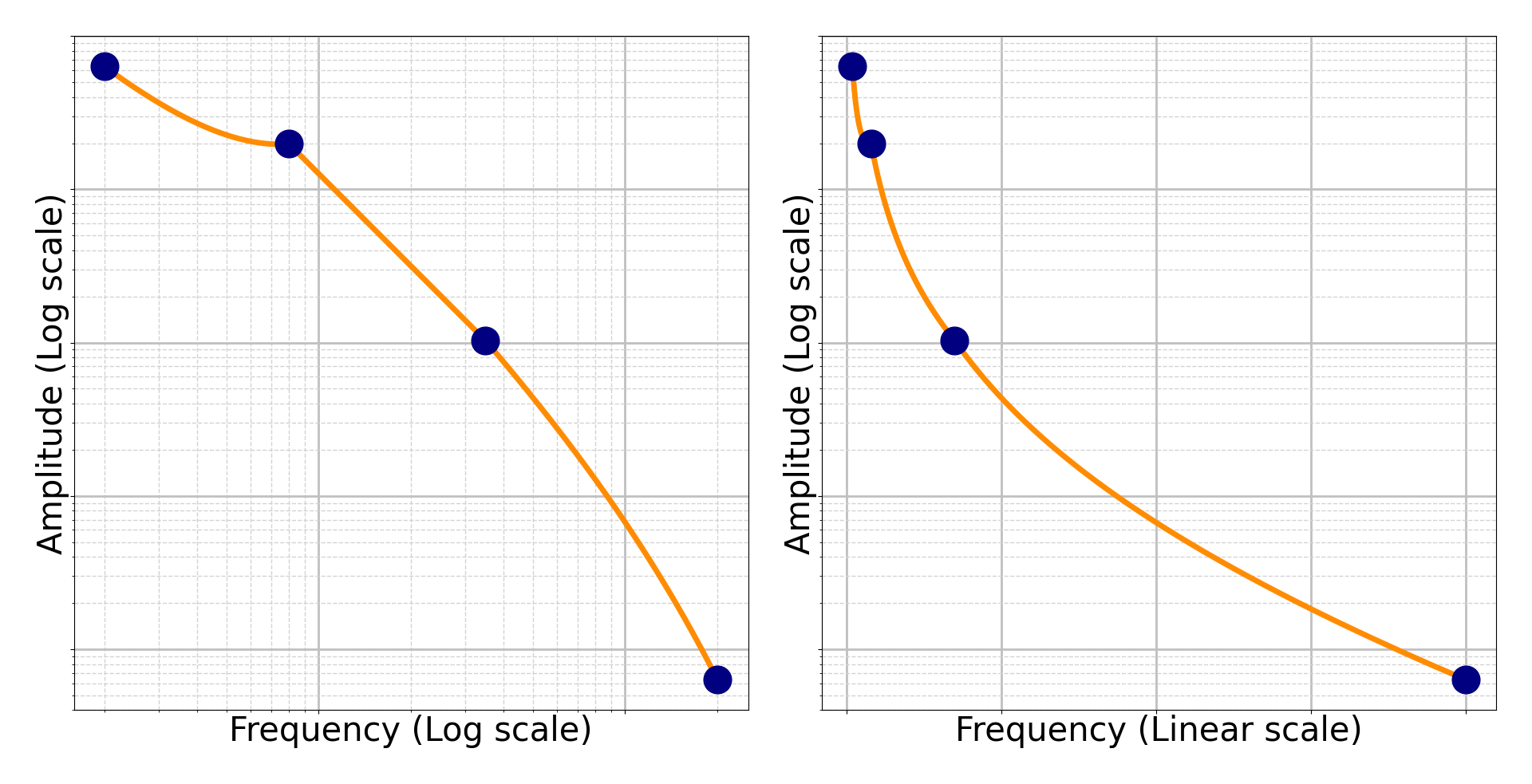
A profile for a Random vibration test, also known as a breakpoint table, is defined as a list of frequency and amplitude values. For example, consider the following breakpoints:
| Frequency (Hz) | Amplitude (EU2/Hz) |
|---|---|
| 20 | 0.01 |
| 80 | 0.05 |
| 350 | 0.05 |
| 2000 | 0.01 |
Let PSD be defined by (fi,Gi) where fi is the frequency (Hz) and Gi is the amplitude (EU2/Hz).
There are two common ways to interpret the frequencies between each breakpoint in the Random profile. The most common method is Log-Log (meaning the log of the amplitudes scales with the log of the frequencies.) Another method is Log-Linear, where the log of the amplitudes scales directly with the frequencies).
In this post, we will show how to calculate the acceleration, velocity and displacement RMS values of a Log-Log and Log-Linear Random profile.
RMS Calculation (Log-Log)
Let (f0, G0), (f1, G1) be the left and right breakpoint for Random PSD.
PSD value G for frequency f where f0 < f < f1:
log(G(f)) = log(G0) + b(log(f) - log(f0))
G(f) = G0(f / f0)b
where:
b = log(G1 / G0) / log(f1 / f0)
Acceleration
PSD is defined as a series of breakpoints (fi, Gi), so the total RMS is calculated as:
To calculate the RMS from frequency range f0 to f1:
If b = -1:
Velocity (Log-Log)
To calculate the RMS from frequency range f0 to f1:
If b = 1:
Displacement (Log-Log)
To calculate the RMS from frequency range f0 to f1:
RMS Calculation (Linear-Log)
Let (f0, G0), (f1, G1) be the left and right breakpoint for Random PSD.
PSD value G for frequency f where f0 < f < f1:
log(G(f)) = af + b
G(f) = eaf + b
where:
Acceleration (Linear-Log)
PSD is defined as a series of breakpoints (fi, Gi), so the total RMS is calculated as:
If G0 = G1, a = 0:
Velocity (Linear-Log)
To calculate the RMS from frequency range f0 to f1:
where Ei is the exponential integral function:
If G0 = G1, a = 0:
Displacement (Linear-Log)
To calculate the RMS from frequency range f0 to f1:
If G0 = G1, a = 0: