I'm still overwhelmed by all this modal stuff Laplace, Fourier, FRFs, and all that! Can you put the big picture together for me?
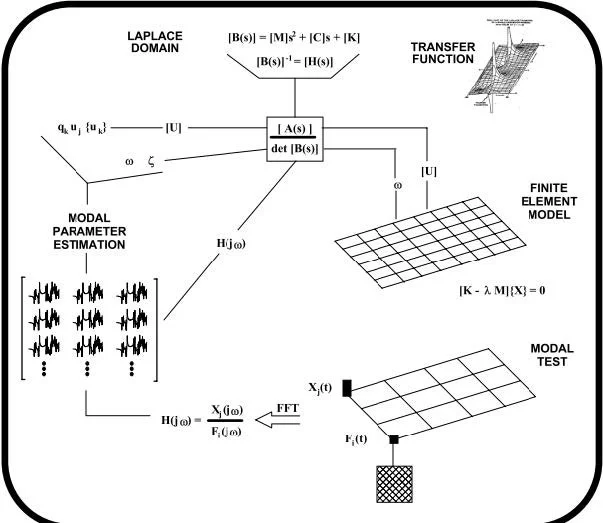
Sure…sometimes it helps to stand back and look at everything from a complete picture. I have a figure that I have used for many years now to help people see things more clearly. I call it "The Big Picture". Let's just look at this picture and discuss all the pieces individually.
First let's start with an analytical representation such as the finite element model shown. Basically, we use the FEM to approximate a lumped mass system that is interconnected by springs to represent the physical system. Since the analytical approximation is described in terms of a force balance for each mass that is described in the system, we end up with one equation for each mass (or degree of freedom) used to approximate the system. Since we need many small little finite elements to accurately describe the system, I end up with many equation and unknowns. Right away, it becomes convenient to describe all these equations using matrices. Now once I have assembled all these equations, a mathematical routine called an eigen solution is used to represent the system in simpler terms - the system's frequencies and mode shapes. This is what we do in the finite element process.
Well, without getting into all the details, I can take those same equations and transform them into the Laplace domain. (No - we don't convert to the Laplace domain to make your life miserable - we do it to make some of the equations easier to handle. Please believe me on this one!) Now in the Laplace domain, we have, [B(s)], the system equation and its inverse, [Hs)], the system transfer function. Now we know that this inverse is the adjoint of the system matrix (or the cofactors of the system matrix) divided by the determinant of the system matrix. This inverse is described in all vibrations text books (usually in Appendix A).
So big deal! What's that mean to you! Well, it turns out that the adjoint matrix contains the modal vectors and we call this the Residue Matrix. The determinant of [B(s)] contains the roots, or poles of the system. Well, this is the same basic information that is obtained from the analytical model. So we could determine the system dynamic characteristics from either the analytical model or from the Laplace domain representation - they both will give the same results.
Now another important relationship is the Frequency Response Function, FRF. This is the system transfer function evaluated along the jw axis. The FRF is actually a matrix of terms, [H(jw)]. Well, since we are dealing with a matrix, it is convenient to identify input-output measurements with a subscript. So a particular output response at point 'i' due to an input force at point 'j' is called hij(jw).
Now remember that the system transfer function has been defined up to this point from mass, damping and stiffness quantities. This function can be computed or synthesized for any input-output combination over any frequency band desired. So if we wanted, we could synthesize several FRFs that make up either one full row or one full column of the FRF matrix if needed or desired as shown in the figure.
Now what we need to realize is that those FRFs that were generated (synthesized) contain information relative to the system characteristics. Remember that the FRFs can be generated from residues and poles. And that the residues are directly related to the mode shapes and the poles are the frequency and damping of the system.
So the parameters that make up the FRFs, are the parameters that we wish to extract from the FRFs. This is what modal parameter estimation is all about. Basically, we use the FRFs in a mathematical algorithm to extract the generic information that makes up the FRFs - the frequency, damping and mode shapes. We often refer to this process as curvefitting. The basic information that is extracted is the mode shapes which are related to information contained in the adjoint matrix or residue matrix and the poles which relate to information in the determinant of the system matrix.
This pretty much summarizes the process - except one important thing needs to be addressed. Up until now we have only discussed using the mass, damping and stiffness approximations to compute system characteristics from the finite element model or from the Laplace domain representation of the system. Both these approaches use approximations of the physical parameters of mass, damping and stiffness to describe the system and so they will both provide the same basic information. If there were some other way to estimate those FRFs without assuming physical properties then I could employ the modal parameter estimation techniques to extract the desired information.
This is where modal testing comes in. Basically, my structure is excited with some measured force. The response of the system due to the applied force is measured along with the force. Now this time data is transformed to the frequency domain using the FFT and basically a ratio of output response to input force is computed to form an approximation of the FRF.
There are many implications of making these measurements which involve digital signal processing concepts which are much too involved to discuss in detail right now (but I think you get the idea where I'm going with all this).
So we could measure one input-output FRF based on this approach. If we used a shaker to excite the structure and move the accelerometer to many points then we could measure a column of the FRF matrix. (If we collected the data using impact techniques then we would measure on row of the FRF matrix). So the big advantage of making measurements is that I measure the response of the system due to the applied force - I don't ever make any assumptions as to the mass, damping and stiffness of the system - and I avoid any erroneous approximations I may make. Of course, I need to make sure that I make very good measurements otherwise I will distort my system characteristics.
So I hope this clears some things up for you. If you have any other questions about modal analysis, just ask me.